证据理论和神经网络结合的诊断方法
证据理论是一种尚未成熟的方法,对它的研究方兴未艾,虽然存在一些缺点,但是其在不确定性推理方面的优良性能,使其在模式识别、故障诊断等许多方面得到了越来越广泛的应用。
本文阐述Dempster.Shafer证据理论的基本原理、两个证据和多个证据的合成方法、基于证据理论的三种决策方法。最后在分析神经网络和证据理论优缺点的基础上,提出了神经网络和证据理论集成的数据融合故障诊断方法。
一、信度函数
1.识别框架
证据理论讨论一个辨识框架。(Frame of Discernment),它是关于命题的相互独立和可穷举的可能答案或假设的一个集合,一般为有限集合。
选取依赖于我们的知识和认识水平。当一个命题对应于该框架的一个子集时,称框架能够识别该命题。按传统方法可以把0的幂集表示为2e,它是所有子集的集合(如果0有Ⅳ个元素,那么2e就有2个元素)。
2.基本信度分配与信度函数
二、证据理论的优缺点
证据理论具有以下一些优点:
1)证据理论具有比较强的理论基础,既能处理随机性所导致的不确定性,又能处理模糊性所导致的不确定性。
2)证据理论可以依靠证据的积累,不断缩小假设集。
3)证据理论能将“不知道"和“不确定”区分开。
4)证据理论可以不需要先验概率和条件概率。而主观贝叶斯方法却需要假设的先验概率和条件概率。
5)证据理论能在不同层次上组合证据,而贝叶斯方法要求有统一的识别框架。
证据理论的主要缺点是:
1)证据理论具有潜在的指数复杂度。
组合两个证据主要要作m×m次相乘,所以计算复杂度为2“X2“,组合k个证据的计算复杂度为k×2“×2“。可见,利用D.S公式合成证据的计算复杂度与证据个数k呈线性关系,与假设集的模n成指数关系。
2)在推理链较长时,使用证据理论很不方便。这是因为在应用证据理论时,必须首先把相应于每个步骤和证据的信度函数变换成一个一般的识别框架,然后再应用Dempster组合规则。当推理步骤增加时,由于最后结果的信度函数的焦元结构的复杂性也相应增加,所以Dempster规则的递归应用就会十分困难。
3)Dempster组合规则具有组合灵敏性。有时,给基本信度分配一个很小的变化都可能导致结果很大的变化。此外,使用Dempster组合规则,要求证据是独立的,这个要求有时使用起来很不方便。
三、证据理论和神经网络集成的数据融合诊断方法
人工神经网络是模仿大脑神经元结构特性而建立的一种非线性动力学系统,它由大量的简单的非线性处理单元高度并联、互连而成,具有很强的数学模拟能力。它以分布存储、并行处理性、容错性、自学习、自组织和自适应性,避免了复杂的建模过程,在故障诊断领域也得到越来越广泛的研究。它在诊断领域的应用主要集中在三个方面:一是从模式识别的角度应用神经网络作为分类器进行故障诊断;二是从预测角度应用神经网络作为动态预测模型进行故障预测;三是从知识处理的角度建立基于神经网络的诊断专家系统。在所有应用的神经网络中,BP网络应用最为广泛,也取得了良好的效果。证据理论以其对不确定性推理的优良特性,也已经在各种故障诊断中被广泛应用,并且与模糊技术等得到了结合运用。
但BP神经网络诊断存在着其固有的缺陷。首先,正确的诊断需要大量的样本训练集,而实际中神经网络训练的大量样本获得是困难的,由此造成了神经网络记忆的诊断知识存在先天性缺陷;其次广泛用于BP神经网络训练的梯度下降训练算法,存在训练速度慢的缺陷,并且随着网络结构复杂度的增加训练时间显著增加;再次由于网络结构的各项参数都是根据经验进行选择,所以很难保证选取的得当,网络的学习和泛化能力难以保障;再者当系统的诊断参数较多,征兆信息量很大时,采用的样本不可避免地存在矛盾性和随机性,此时若将高维的征兆信息同时输入到同一网络处理,不但训练时间长,而且训练效果差,有时甚至导致网络不收敛,这些都极大影响了神经网络的诊断效果。
为了克服神经网络的缺陷,可以如同人脑中不同区域处理不同的信息一样,不同的信号也应由各自的神经网络来诊断,这样就能将高维的征兆空间分解为较低维的征兆空间。将复杂的网络变成简单的网络,由不同的神经网络处理不同的低维征兆空间得到诊断结果,因此简化了网络结构,提高了网络训练的速度。因为简单的网络,只处理问题的某一方面,样本容易获得、结构容易确定,训练的速度可以提高,网络的泛化能力增强,诊断效果有保证。可是这样并没有充分利用不同征兆空间(在证据理论中成为证据空间)的信息。因此为了充分利用这些信息,可以对各子网络的诊断结果利用证据理论进行故障信息的融合处理。
而且证据理论的基本信度分配,是专家在所获证据的基础上,根据个人的经验对识别框架中不同命题的支持程度的数字化表示,主观性很强。因此,对同一个证据对同一个命题不同的专家会给出不同的信度分配,有时差别很大。为了更客观地得到一证据对不同的命题的支持度的大小,可以将各个独立的低维的神经网络作为证据理论的一个证据,并把低维神经网络的输出值转化作为辨识框架上命题的基本可信度。经过证据理论的再次融合,类似于神经网络对信号层面数据的特征提取后的特征值再加以融合,充分利用证据源的信息,将大大提高识别的准确率,消除单一传感器包含信息的不全面和模糊性,因为证据理论可以对多个证据都支持的判断进行加强。
根据监测系统的情况把传感器分成独立的组,对每个测点的传感器或传感器组,对应一个局部神经网络进行局部诊断。这样可以简化各个网络,网络更小更简单,避免了单一诊断神经网络复杂的结构形式,以及某一传感器故障或数据源的错误对整个诊断系统带来的不良影响,诊断系统的容错性能增强,其原理如图6所示。
若诊断系统的诊断故障域为g个故障状态,对应证据理论的识别框架0就包括g个故障状态及系统的正常状态。同时,若系统共有p个局部诊断神经网络,每个网络对应的输出同样为g+1个,分别对应g个故障状态及系统的正常状态。每个神经网络作为证据理论的一个独立证据,将神经网络的输出值经过变换,成为此证据下各种状态的可信度分配,为证据合成奠定基础。每个诊断网络诊断的能力是不同的,因此每个网络存在一个可靠性系数理(即证据的折扣),表示了对判定结果的信任程度。
征兆空间 故障空间
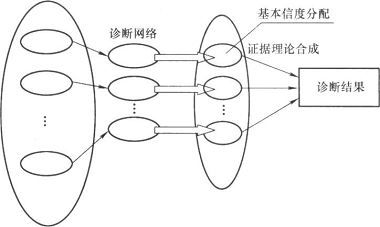
图6神经网络证据理论诊断模型
设第i个网络的第歹个输出值,那么它对应的在本证据的基础上的对状态,的信度分配;所以经过证据合成后各状态的置信区间[Bel,P1],并由此进行诊断状态判断。这里采用以下判决原则:
证据理论可以使多个证据都支持的命题合成后的信度提高,减小未知信度,从而减小判断的模糊性,达到提高诊断准确率的目的。
将证据理论和神经网络相结合应用于故障诊断系统中就可以实现优势互补、扬长避短。神经网络和证据理论集成方法除具有一般神经网络的性质和特点外,还具有一些特殊性质。比如,由于采用了证据理论中的不确定性推理方法,避免了贝叶斯推理无法区分“不知道”和“不确定”信息,也不需要明确先验概率和条件概率。同时克服了证据理论基本信度分配主观性过强的缺陷,这使得系统的诊断能力得到明显加强。
